カルダノ(ADA)のステーキングとは、ADAを保有するだけでADAがもらえるしくみです。
誰でも簡単!カルダノ(ADA)ステーキングの方法としくみ
ところで、どこから報酬のADAは湧いてくるの?と疑問をお持ちの方も多いのではないでしょうか。
そこでこの記事では、カルダノのステーキング報酬分配の流れや計算式を解説します。
まず簡単に全体の流れを紹介してから、後半で具体的な計算方法を解説します。
ADAのステーキング報酬分配の流れ
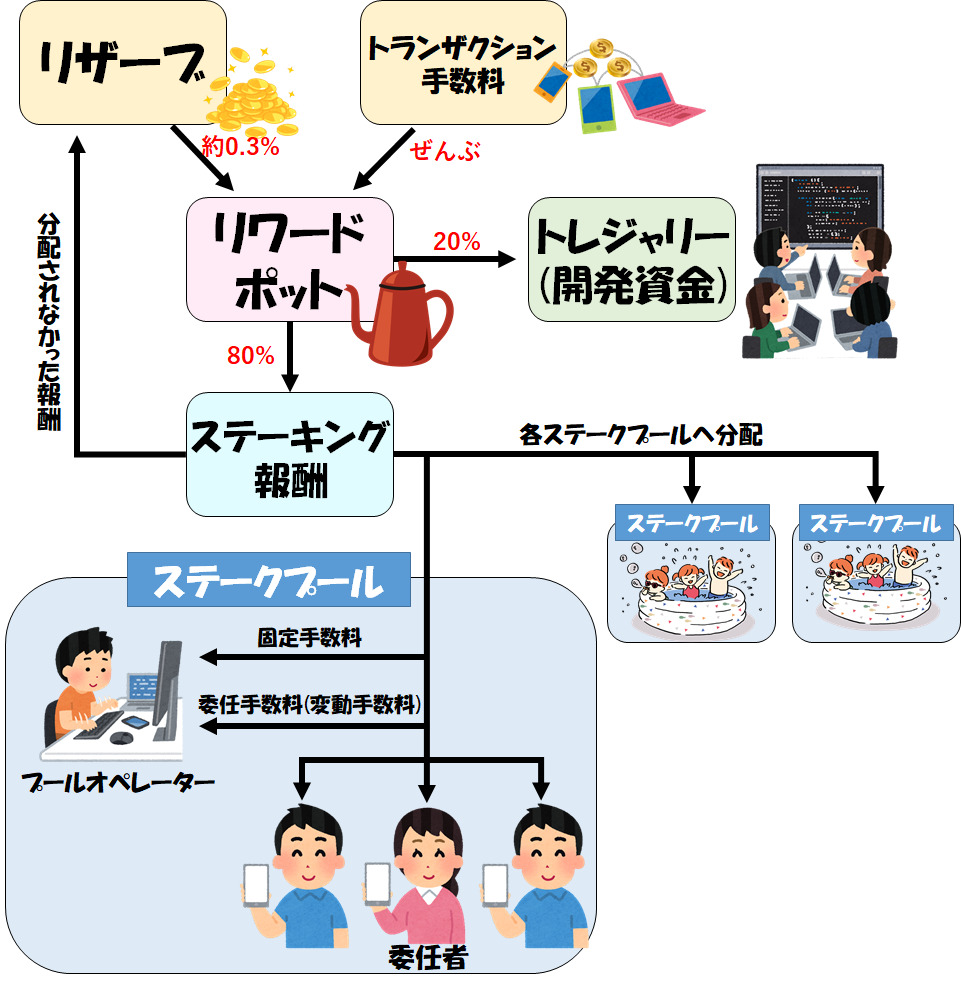
ADAのステーキング報酬の分配は、下の図のような流れで行われています。
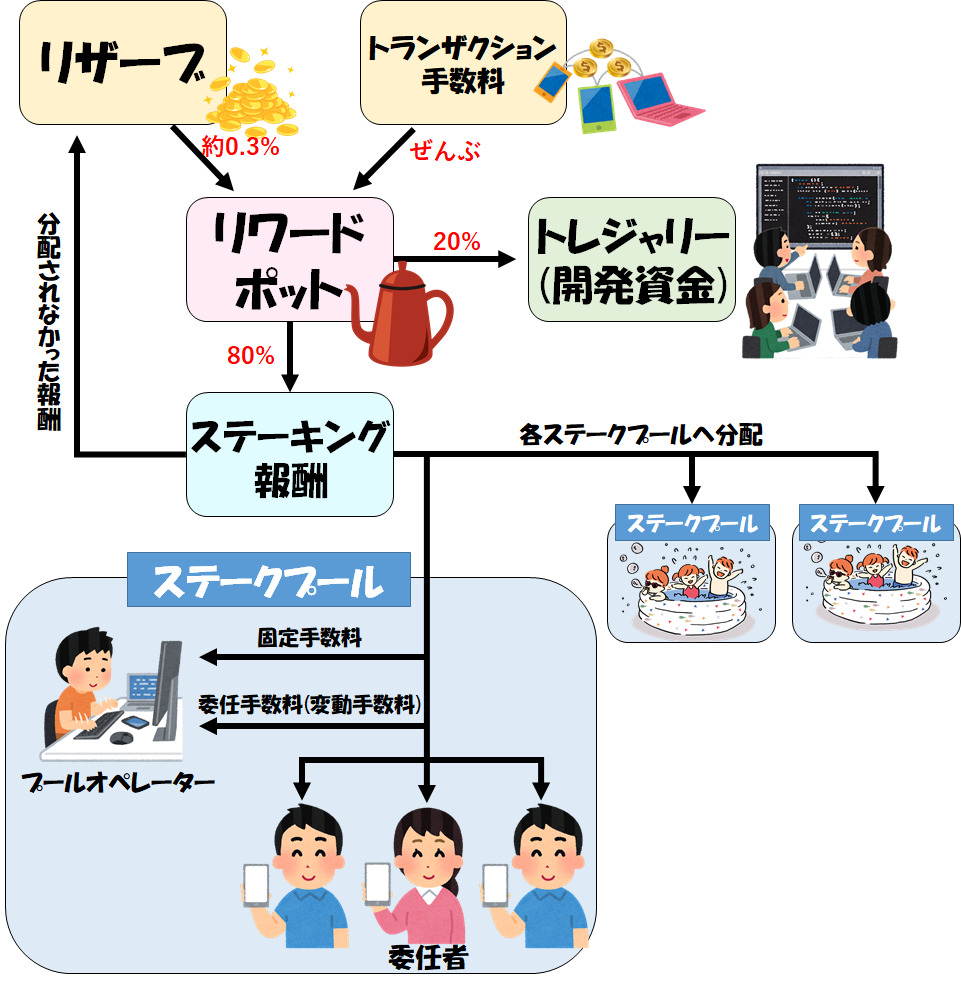
いきなりすべてを理解するのは大変なので、まずは上半分から見ていきましょう。
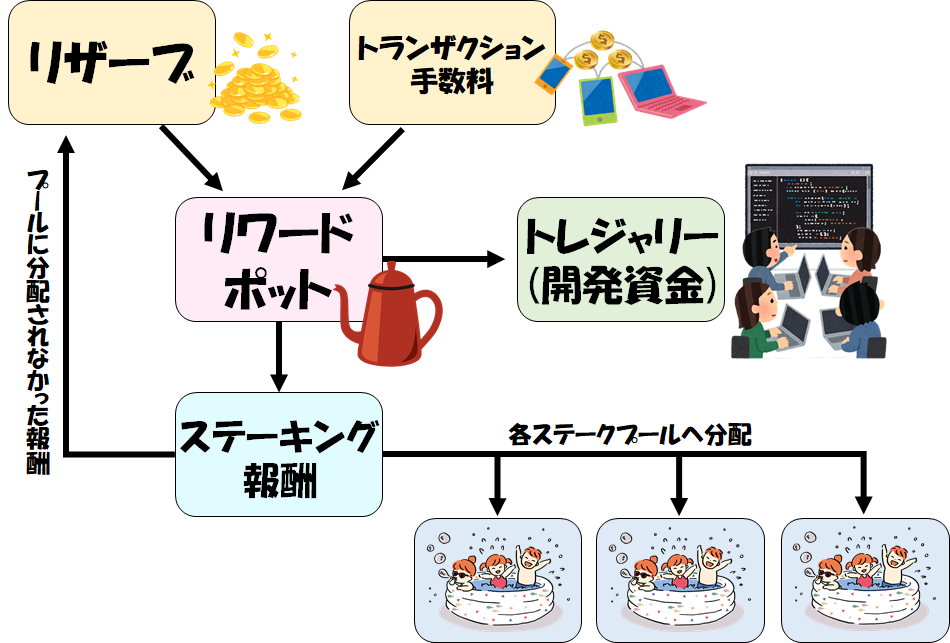
リザーブとトランザクション手数料からリワードポットへ
ADAのステーキング報酬は、「リザーブ」「トランザクション手数料」の2つから供給されています。
- リザーブ
まだ市場に出回っていないADA(未発行のADA)です。
2021年9月現在、発行上限450億ADAに対し、すでに約330億ADAが市場に出回っています。残りの約120億ADAがまとめてリザーブと呼ばれます。
毎エポックでリザーブの残高の約0.3%がリワードポットに払い出されます。 - トランザクション手数料
主にADAを送金する際にかかる手数料です。
毎エポックでトランザクション手数料のすべてがリワードポットに集められます。
※IOHKのペーパーでは3つめの供給元としてデポジットが挙げられていますが、こちらについては記事の最後で検討します。
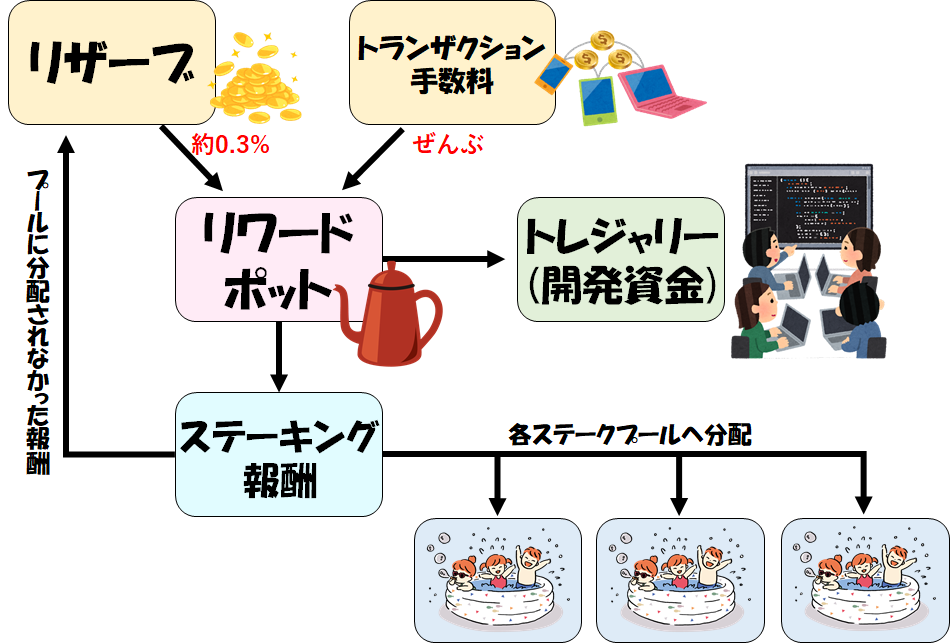
さて、ステーキング報酬の元となるADAがリワードポットに集められました。
2021年9月現在、毎エポックでリワードポットに集められる総額は約3600万ADAですが、そのほとんどはリザーブから来ています。トランザクション手数料の合計は数万ADAとわずかです。
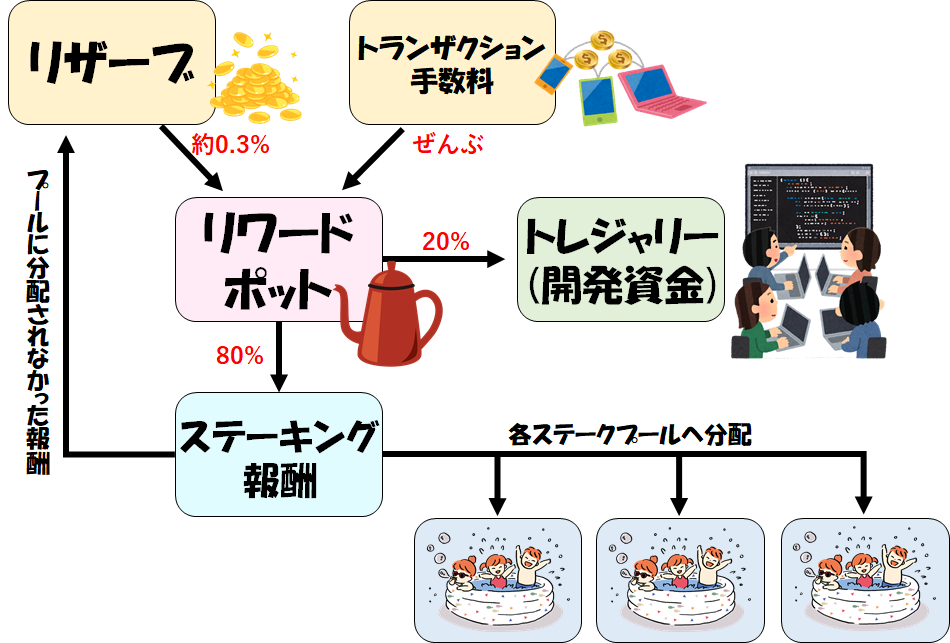
リワードポットからトレジャリーとステーキング報酬へ
リワードポットに集められたADAのうち、20%はトレジャリーに送られ、残りの80%がステーキング報酬に割り当てられます。
- トレジャリー(treasury)
カルダノの価値を高める開発を支援するための資金です。
2021年9月現在、カタリスト(Project Catalyst)という投票システムにより、カルダノに貢献するプロジェクトへの資金提供が行われています。
毎エポックでリワードポットのうちの20%がトレジャリーに蓄えられます。 - ステーキング報酬
ステーキングによってカルダノネットワークを支えている皆さんに対して支払われる報酬です。
毎エポックでリワードポットの80%がステーキング報酬に充てられます。
そのすべてがステーキング報酬として分配されるわけではなく、現状では半分近くが再びリザーブに戻っています。詳しくは後ほど、計算式のところで解説します。
各ステークプール・委任者への報酬分配
ステーキング報酬は各ステークプールに分配されます。
各プールへ分配される報酬の量は、主に以下の要素によって決まります。
- プールがそのエポックで生成したブロックの数
- プールへの委任量
- 誓約(プールオペレーターによるプールへの委任量)
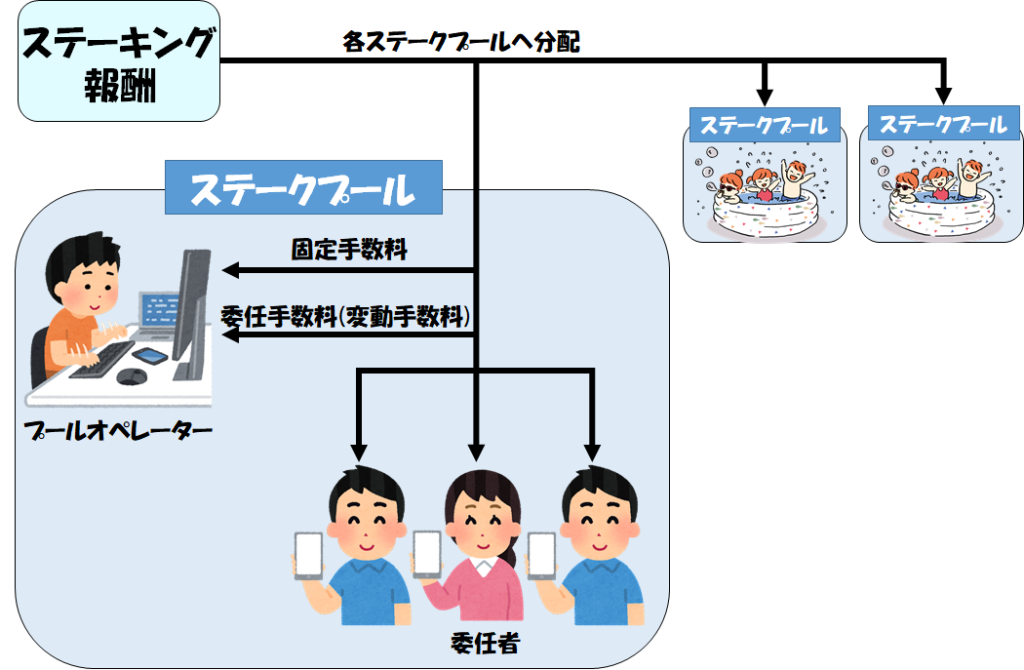
各プールへ分配された報酬の中から、そのプールを運営するオペレーターに2種類の手数料(報酬)が支給されます。
手数料は各プールオペレーターが独自に設定するため、プールによって設定値が異なります。
- 固定手数料(fixed cost)
プールに分配された報酬のうち、オペレーターがもらう固定の報酬です。多くのプールは最低額の340ADAを固定手数料としています。 - 委任手数料(margin)
プールに分配された報酬から固定手数料を引いた残りのうち、オペレーターが一定の割合でもらう報酬です。委任手数料は0%~100%の間で設定できますが、多くのプールは0%~5%です。
「手数料」という名目ではあるものの、委任者が直接支払うわけではありません。オペレーターの報酬はプール全体の報酬から差し引く形で支給されています。
プール全体の報酬から2種類の手数料が引かれた残りが、ステーキング報酬として委任者に分配されます。
各委任者へ分配される報酬の量は、それぞれが委任している量に比例します。
例えばプールに500ADAを委任しているAさんは、同じプールに100ADAを委任しているBさんの5倍の報酬を受け取ります。
以上がステーキング報酬分配の流れです。
ADAのステーキング報酬分配の計算方法
ここからは、ステーキング報酬の分配がどのようなパラメータや計算式によって行われているのかを見ていきましょう。
具体例として、当プールMIYABI KYOTOがエポック287で生成したブロックによる報酬分配計算を行います。
リザーブとトランザクション手数料からリワードポットへ

毎エポックでリザーブからリワードポットへ供給されるADAは、以下の式で計算されます。
$min(η, 1)ρ(T_{\infty}−T)$
$η$ : そのエポックで実際に生成されたブロック数が、ブロック生成数の期待値に占める割合
$ρ$ : リザーブから排出される割合を決定するパラメータ。2021年9月現在$ρ=0.003$
$T_{\infty}$ : ADAの発行上限 $45,000,000,000$
$T$ : $T_{\infty}$のうち、すでに市場に出回っているADA
つまり$(T_{\infty}−T)$がリザーブの残高であり、そこに排出率$ρ=0.003$とエポックのブロック生成実績$η$が掛けられることで、リザーブから排出されるADAの枚数が決まります。
$η$は期待値1を上回る可能性もあるので、$min(η,1)$とすることでADAの供給数が発行上限を超えないようになっています。
実際に計算をする上での難題は$(T_{\infty}−T)$の設定ですが、ここでは$(T_{\infty}−T)=11882381119$とします。詳しくは記事の最後で検討したいと思います。
リザーブからリワードポットへ排出されたADAを計算しましょう。
$min(η, 1)ρ(T_{\infty}−T)$
$=\frac{21065}{21600} \cdot 0.003 \cdot 11882381119$
$\fallingdotseq 34764199$
リワードポットのもう一つの供給元はトランザクション手数料です。
エポック287で回収されたトランザクション手数料は86536ADAなので、これをすべてリワードポットに足します。
$34764199+86536=34850735$
リワードポットの金額を求めることができました。
リワードポットからトレジャリーとステーキング報酬へ
このパートの計算は簡単です。
リワードポットのうち、$\tau=0.2$すなわち20%がトレジャリーに積み立てられ、残りの80%はステーキング報酬に回されます。

ステーキング報酬$R$を求めます。
$R=34850735 \cdot 0.8=27880588$
各ステークプールへの報酬分配
ここからの計算はちょっと大変ですが、気合いを入れて頑張りましょう。

あるプールに分配される報酬$\hat{f}$は、以下の式で計算されます。
$\hat{f}(s, σ, \bar{p})=\bar{p}f(s, σ)$
$\bar{p}$ : そのプールのパフォーマンス値(ブロック生成の期待値に対し、実際は何ブロック生成したか)
$f(s, σ)$ : そのプールに分配される報酬の最適値(期待値)
それぞれの値は以下の式で求められます。
$\large{\bar{p}=\frac{n}{max(1, \bar{N})σ_{a}}}$
$\large{f(s, σ)=\frac{R}{1+a_{0}} \cdot (σ’+s’ \cdot a_{0} \cdot \frac{σ’-s’ \frac{z_{0}-σ’}{z_{0}}}{z_{0}})}$
$n$ : エポックでそのプールが生成に成功したブロックの数
$\bar{N}$ : エポックですべてのプールが生成に成功したブロックの合計数
$σ_{a}$ : 総ステーク量に占めるそのプールのステークの割合
$R$ : ステーキング報酬(リワードポットの80%)
$a_{0}$ : オペレーターの誓約がプールの報酬に与える影響を決めるパラメータ。2021年9月現在$a_{0}=0.3$
$z_{0}$ : 飽和したプールが市場に出回っているADA($T$)に占める割合、すなわち$\frac{1}{k}=\frac{1}{500}=0.002$
$s$ : 市場に出回っているADA($T$)のうち、そのプールのオペレーターの誓約が占める割合
$s’$ : $min(s,z_{0})$
$σ$ : 市場に出回っているADA($T$)のうち、そのプールに委任されたADAの割合
$σ’$ : $min(σ,z_{0})$
まず上の式から見ましょう。
$\large{\bar{p}=\frac{n}{max(1, \bar{N})σ_{a}}}$
$\large{=\frac{n}{max(1, \bar{N})} \div σ_{a}}$
式の左側$\frac{n}{\max(1,\bar{N})}$は、そのプールが生成したブロックが、全体のブロック数に対してどのくらい多いかを表します。
右側の$σ_{a}$は、そのプールのステーク量が、全体のステーク量に対してどのくらい多いかを表します。
つまりこの計算では、あるプールがカルダノ全体に占めるステークの割合とブロック生成数の割合を比較し、ステークの割合に対してブロック生成数の割合は何倍か?というパフォーマンス値$\bar{p}$を求めています。
次は下側の式です。
$\large{f(s, σ)=\frac{R}{1+a_{0}} \cdot (σ’+s’ \cdot a_{0} \cdot \frac{σ’-s’ \frac{z_{0}-σ’}{z_{0}}}{z_{0}})}$
この計算では、そのプールがステーク量から算出されるブロック生成数の期待値と全く同じブロック数を生成した時にもらえる報酬$f(s, σ)$を求めています。
$s’=min(s,z_{0})$, $σ’=min(σ,z_{0})$とすることで、飽和を超えた分のステークが報酬に与えるメリットはゼロになっています。
オペレーターの誓約が市場に出回っているすべてのADAに占める割合$s’$は、多くの場合無視できるほど小さいです。$s’=0$として式を簡単にしてみましょう。
$\large{f(s, σ)=\frac{R}{1+a_{0}} \cdot σ’}$
誓約の影響を無視すれば、あるプールがもらえる報酬の期待値は、そのプールのステーク量に比例することがわかります。
これら$\bar{p}$と$f(s, σ)$を掛ける、すなわち標準的な報酬量にパフォーマンス値を掛けることで、あるプールが実際に貰える報酬の量が求められます。
$\hat{f}(s, σ, \bar{p})=\bar{p}f(s, σ)$
それでは実際にMIYABI KYOTOのエポック287の報酬を計算してみましょう。どのタイミングの$σ’,s’$を用いるかが不透明ですが、ステーク量の決定するエポック286の始めのスナップショット時の値を代入してみます。
$\large{\bar{p}=\frac{n}{max(1, \bar{N})σ_{a}}}$
$\large{=\frac{7}{21065 \cdot \frac{4967251}{23041103352}}}$
$\fallingdotseq 1.54143$
$\large{f(s, σ)=\frac{R}{1+a_{0}} \cdot (σ’+s’ \cdot a_{0} \cdot \frac{σ’-s’ \frac{z_{0}-σ’}{z_{0}}}{z_{0}})}$
$\large{=\frac{27880588}{1+0.3} \cdot (\frac{4967251}{33050654414}+\frac{400}{33050654414} \cdot 0.3 \cdot 0.0751404)}$
$\fallingdotseq 3223.26$
$\hat{f}(s, σ, \bar{p})=\bar{p}f(s, σ)$
$=1.54143 \cdot 3223.26$
$\fallingdotseq 4968.43$
MIYABI KYOTOのエポック287の報酬合計は4968.43ADAという計算結果が出ました。
ADApoolsやCardanoscanでは報酬額が4970.85ADAとなっているので、かなり近い計算結果です。ただ、やはり少しズレが生じているようですね。
手数料はさておき、委任量4967251ADAに対して約4970ADAという報酬割合を73乗して年利換算すると7.57%です。
ただし、エポック287の報酬期待値$f(s, σ)$約3223ADAを年利換算すると4.85%です。
$η=1$としてカルダノ全体のブロック生成数の影響を無くしても、年利は4.97%にとどまります。
誓約が0から100万ADAに増えても年利は0.025%ほどしか増えないので、現在多くのプールの年利の期待値は5%を切っていることがわかります。
オペレーター・委任者への報酬分配
最後にプール全体の報酬$\hat{f}$をオペレーターと委任者で分配します。

オペレーターは固定手数料(fixed cost)・委任手数料(margin)の順で、プール全体の報酬の中から報酬をもらいます。
もし固定手数料がプール全体の報酬を超える場合、プールの報酬のすべてがオペレーターに入ります。
MIYABI KYOTOでは固定手数料340ADA・委任手数料0%としているので、
オペレーター報酬 : 340ADA
委任者の報酬合計 : 約4630ADA
となります。この4630ADAを、委任量に応じて分配します。
例えばプールの総委任量4967251ADAに対して10000ADAを委任している方の場合、
$4630 \cdot \frac{10000}{4967251} \fallingdotseq 9.321$
約9.321ADAをエポック287分の報酬としてエポック289で受け取ったことになります。
以上、ステーキング報酬分配の計算方法でした。
ステーキング報酬の分配率とリザーブの減少率の関係
現状ではかなりの量のステーキング報酬$R$が分配されずに余っています。
報酬$R$が余る原因は2つあります。
- 市場に出回っているのにステーキングされていないADAがある
- プールの誓約が飽和量より小さい
2021年9月現在ステーキングされているADAは流通量の約71%です。
すべてのプールの誓約が無視できるほど小さい場合、プールに分配される報酬の合計は、$a_{0}=0.3$を用いて以下のように推定できます。
$\displaystyle \sum_{pools} f(σ)=\frac{R}{1+a_{0}} \cdot \sum_{pools}σ’$
$=\frac{R}{1+0.3} \cdot 0.71$
$\fallingdotseq 0.546R$
$R$のうち、プールに分配されずに余った報酬はリザーブに再び戻ります。
つまり現状では、毎エポックで$R$の約45%が分配されずにリザーブに戻っていることになります。
そのため、$ρ=0.003$に対し、リザーブの実際の減少率は$0.0019$程度になっています。
リザーブの減少率が$ρ$と同じ$0.003$になるためには、以下の条件をすべて満たす必要があります。
- $k=500$個のプールのみにADAがステーキングされている
- すべてのプールが飽和しており、誓約が飽和量と等しい
- エポックで期待値以上のブロック数が生成される(スロットバトルやハイトバトルがほとんど無い)
実現不可能です。
誓約とステークプール報酬の関係
誓約が多いほどプールの報酬も増えることは有名です。特に飽和に近いステーク量を持つプールでは、誓約が多いほどプールの報酬も多くなります。
しかしプールのステーク量が少ない場合、逆に誓約が多すぎることで報酬が減ります。
例えば委任量1,000,000ADAのプールで、誓約500,000ADAと誓約1,000,000ADAの場合の報酬期待値を比較してみましょう。
流通しているADAの量を2021年9月現在の値に近い330億ADAとします。
誓約500,000ADAの場合
$\large{f(s, σ)=\frac{R}{1+a_{0}} \cdot (σ’+s’ \cdot a_{0} \cdot \frac{σ’-s’ \frac{z_{0}-σ’}{z_{0}}}{z_{0}})}$
$\large{=\frac{R}{1+0.3} \cdot (\frac{1000000}{33000000000}+\frac{500000}{33000000000} \cdot 0.3 \cdot 0.007690542)}$
$\fallingdotseq 0.0000233369R$
誓約1,000,000ADAの場合
$\large{f(s, σ)=\frac{R}{1+a_{0}} \cdot (σ’+s’ \cdot a_{0} \cdot \frac{σ’-s’ \frac{z_{0}-σ’}{z_{0}}}{z_{0}})}$
$\large{=\frac{R}{1+0.3} \cdot (\frac{1000000}{33000000000}+\frac{1000000}{33000000000} \cdot 0.3 \cdot 0.0002295684)}$
$\fallingdotseq 0.0000233116R$
この場合、誓約を500,000ADAから1,000,000ADAに増やすことで、報酬が0.1%ほど減ってしまうことがわかります。
プライベートプールを運営されている方は、誓約の量を見直してみると利率が上がるかもしれません。
検討が必要な点
デポジット
今回参考にしたIOHKのペーパー “Design Specification for Delegation and Incentives in Cardano”では、リワードポットの供給元の3つ目として”decayed deposits”が挙げられていますが、返却されないデポジットというのは聞いたことがありません。
こちらのIOHKのGitHubを見る限りではデポジットの減衰システムは無くなったようですが、詳しい情報を知っている方がいらっしゃったらご連絡ください。
T(市場に出回っているADA)
それぞれの計算で、どのタイミングの$T$を計算に用いるかが曖昧です。ブロック生成に用いるステークが登録されるエポックなのか、ブロックを生成したエポックなのか、その後で報酬計算をするエポックなのか。また、そのエポックで配られる報酬が分配される前なのか、分配された後なのか…。
ADAの供給数が発行上限を超えないためには、報酬を分配するタイミングでリザーブ残高を参照するべきだと考えます。よってリザーブからの払い出しの際は、報酬計算をするエポックで報酬が分配された後のリザーブ残高を参照してみました。すなわちエポック288において、エポック286で生成したブロック分の報酬が分配された後のリザーブ残高です。
IOHKのペーパーには
T is the amount of ada in circulation at the beginning of the epoch for which we want to calculate the rewards pot
https://hydra.iohk.io/build/3744897/download/1/delegation_design_spec.pdf
とありますが、正直よくわかりません。有識者の皆様のご意見をお待ちしております。
また、$σ’,s’$を求めるタイミングも曖昧です。報酬計算時の$T$は、2エポック前でステークが登録されるスナップショット時の$T$よりも多いので、$σ’,s’$を求める際に報酬計算時の$T$を用いるのは変な気がします。よって今回$σ’,s’$はエポック286の始めのスナップショット時の値を用いることにしました。
本気で答えを知りたいならウロボロスのソースコードを読むしかなさそうです。


